Zurück zum Menü 2 2.0.17 Die demokratische Gruppe Erste Fassung: 29.03.2010 |
|
|
Über
das
demokratische
Grundelement.
Ausgehend
von diesem
Artikel möchte ich hier
noch einmal das demokratische Grundelement
hervorheben und einmal
kürzer erläutern:
Wir hatten es mit folgender Grafik zu tun: In
dieser Grafik haben wir es
mit drei demokratischen Grundelementen
zu tun. Drei mal drei Leute.
Jede Gruppe berät für sich, wählt einen
Sprecher. Diese
Sprecher bilden ja dann wieder ein
demokratisches Grundelement aus drei
Leuten. Dann wird wieder beraten und ein
letzter Sprecher gewählt.
Es gibt bei 9 Personen also 2 Beratungsdurchgänge die ich hier einmal Iterationen nenne. Man sieht auch, dass sich eine stabile Iterationsmöglichkeit bei einer Personenanzahl von jeweils 3 hoch X ergibt. Also als Beispiele:
und so weiter, und so weiter .... Hierbei haben wir es mit einem Gebilde wie bei einem Sirpinski-Teppich im entferntesten Sinne zu tun, nur dass die Iterationsvorschrift zum Aufbau der sicheren Werte einfach " 3 hoch X" heißt. Die
Iterationsvorschrift
für die demokratischen
Erörterungen heißt dann etwa
so:
Der Exponent "X" bei "3 hoch X" zeigt dabei schon mal vorab die nötigen Iterationen, also die nötigen Durchgänge an, bis die Ergebnisverkündung stattfinden kann. Man kann also umgekehrt schon einmal die dritte Wurzel der Teilnehmerzahl nehmen, um die nötige Anzahl der Durchgänge zu berechnen. Hier einmal die Grafik für die demoktratische Menge "81": Dritte Wurzel aus 81 ==> 4 Hierbei würden also 4 Druchgänge a 10 Minuten benötigt, also würde die Meinung nach etwa 40 Minuten gut erörtert und gefunden sein. Lächerliche
40
Minuten. --- Bei 81 Personen in
diesem Beispiel.
Rechnen wir eine Stunde, dann kommt das ganz gut hin. Sehr
flott eigentlich, wenn das
einmal mit den politischen Debatten
von 2000 bis 2010 vegleicht ...
Demokratie mit Prozess-Sicherheit und vor allem Produktivität. 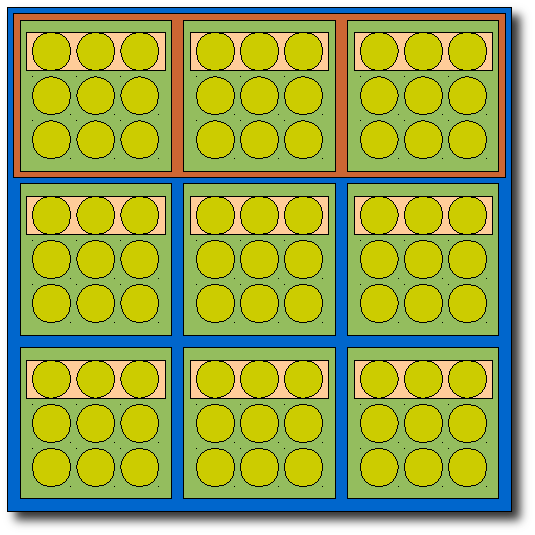 "81-er Meinungs-Menge" Mit den verschiedenen Farben ist die Verschachtelung der demokratischen Grundelemente (3-er), der Gruppen (9-er) und des Clusters (27-er) gut zu sehen. Man sieht hier also gut die Selbstähnlichkeit der verschiedenen "Ebenen". Mein Favorit ist jedoch diese Darstellungsweise:  "9er-Meinungs-Gruppe" Hier sehen die Meinungen der Konferenzteilnehmer schon nicht mehr so "zementiert" und starr aus. Auch hier gibt es zwei Konferenzdurchläufe und dann eine Meinungsverkündung. Man sieht gut, wie sich Meinungen ändern und verschieben können. Die Schachtelung erfolgt hier nicht nebeneinander, sondern jede(r) ist mit jede(m/r) verbunden. Abschließend zeige ich an der folgenden Video-Bastelei, wie man eine Polarisation auflösen, bzw. vermeiden kann. Ich bitte alle Entscheidungsträger das zu berücksichtigen, denn es ist stabil und sehr eigensicher. ---------------------------------------------------------------------------------------------------
Ich wünsche
Gute, weise
Entscheidungen,
 |
|
|
|